Entropy & the Reality Dimension: How QTT Rewrites the Second Law

Posted byQuantum Traction Theory 1 Comment on Entropy & the Reality Dimension: How QTT Rewrites the Second Law

Reference of this blog https://doi.org/10.5281/zenodo.17594186

In standard physics, entropy is a slippery concept. Sometimes it’s “disorder,” sometimes it’s “information,” sometimes it’s a probability over microstates. We write

S = -k_B \sum_i p_i \ln p_i

or, in quantum language,

S = -k_B \mathrm{tr}(\rho \ln \rho),

and then we say the “Second Law” claims that this entropy increases for closed systems, at least in practice.

Quantum Traction Theory (QTT) takes a very different route. Instead of defining entropy from probabilities or coarse-graining, it builds entropy directly from the geometry of the Reality Dimension and from how world–cells are created and populated over time.

In this picture:

  • Entropy becomes an anchored modular charge defined per world–cell address w (in the Reality Dimension).
  • There is a fixed budget of “modular charge” per address – a 2\pi bundle budget.
  • The Second Law comes from the creation of new addresses (new world–cells in the Reality Dimension), not from probabilistic typicality.
  • The familiar area law and finite black–hole entropy become natural consequences of finite capacity per address.

1. World–cell addresses and the Reality Dimension

In QTT, the Reality Dimension (labelled by w) is a “reality index” that tells you where in the world–cell ledger a bundle actually lives. The physical Hilbert space factorises by these addresses:

\mathcal H = \bigotimes_w \mathcal H_w,<br /> \qquad<br /> \mathcal H_w = \mathcal H^{\mathrm{vis}}_w \otimes \mathcal H^{\mathrm{hid}}_w.

Each address w comes with a visible sector (what we see) and a hidden sector (Reality Dimension degrees of freedom that we don’t directly observe). The Reality Dimension controls how capacity and modular flow are split between visible and hidden parts of each world–cell.

Choose a reference (equilibrium-like) state \omega_w at each address. The modular structure (Tomita–Takesaki) associated to this state gives a modular Hamiltonian K_{\omega,w} = -\ln \omega_w. QTT then defines a local anchored modular charge using relative entropy.

2. Entropy as anchored modular charge per Reality–Dimension address

For a state \rho_w at address w, the QTT “anchored modular charge” is

Q_w(\rho_w \Vert \omega_w)<br /> := 2\pi\, S(\rho_w \Vert \omega_w)<br /> = 2\pi\left(\mathrm{tr}\,\rho_w \ln \rho_w - \mathrm{tr}\,\rho_w \ln \omega_w\right) \ge 0.

Here S(\rho_w \Vert \omega_w) is the usual Umegaki/Araki relative entropy. The key shift is this:

  • Entropy is not “disorder” in a gas; it is a modular charge anchored at each Reality–Dimension address.
  • The total visible QTT entropy is a sum over addresses:
S_{\mathrm{QTT}}^{\mathrm{vis}}[\rho]<br /> := k_B \sum_w S(\rho_w^{\mathrm{vis}} \Vert \omega_w^{\mathrm{vis}}).

This functional is automatically nonnegative and monotone under admissible (CPTP) maps on the visible sector, which makes it a robust, coordinate-free notion of entropy.

So entropy in QTT = “how far each visible state is, at each Reality–Dimension address, from its reference modular equilibrium,” measured in anchored modular charge units.

3. Axiom A7: a 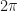2\pi budget per world–cell in the Reality Dimension

QTT’s Axiom A7 (Law of Bundled Existence) says that existence at an address w comes as a bundle of visible + hidden shares that together exactly saturate a full modular circle:

Q_w^{\mathrm{bundle}} = 2\pi,<br /> \qquad<br /> 0 \le Q_w^{\mathrm{vis}} \le 2\pi,<br /> \qquad<br /> Q_w^{\mathrm{vis}} + Q_w^{\mathrm{hid}} = 2\pi.

In other words:

  • Each Reality–Dimension address w has a fixed budget of anchored modular charge: 2\pi per world–cell.
  • Visible and hidden shares can exchange, but the total per address is always limited.

This is a drastic difference from standard field theory, where local entanglement entropy diverges and has to be regularised. In QTT the Reality Dimension imposes a hard cap per address: no more than one modular circle’s worth of charge.

4. Creation in the Reality Dimension and a global Second Law

QTT also has a Law of Creation: white–void “seeds” generate new space quanta (new world–cells, new Reality–Dimension addresses) at a rate tied to the underlying Planck scales. Each new space quantum (each new address w) arrives with its own 2\pi modular budget.

Define the total QTT entropy (visible + hidden) as

S_{\mathrm{QTT}}^{\mathrm{tot}}(T)<br /> := \frac{k_B}{2\pi}\sum_{w\in \mathcal W(T)} Q^{\mathrm{bundle}}_w<br /> = k_B N_{\mathrm{addr}}(T),

where N_{\mathrm{addr}}(T) is the number of active addresses (world–cells) at Absolute Clock time T. Because the Law of Creation increases N_{\mathrm{addr}} in time, we have

\frac{d}{dT} S_{\mathrm{QTT}}^{\mathrm{tot}}(T)<br /> = k_B \frac{dN_{\mathrm{addr}}}{dT} \ge 0.

This is a very strong statement:

  • The global entropy increases because the Reality Dimension creates new addresses, each loaded with capacity budget.
  • This entropy production does not depend on coarse-graining or probability; it is purely geometric and address-counting.
  • The “arrow of time” is tied directly to the growth of the Reality–Dimension ledger of world–cells.

So the Second Law is no longer a statistical “most of phase space” argument; it’s a creation-driven fact about how the Reality Dimension expands the ledger.

5. Local Second Law: KMS, Reality Dimension, and Clausius inequality

At each address w, when the visible sector is close to a thermal fixed point

\omega_w^{\mathrm{vis}} \propto e^{-\beta H_w},

the QTT dial geometry enforces a KMS condition under an imaginary rotation of the dial parameter (Reality Dimension “Wick rotation”):

t \to -J\beta \hbar.

Positivity of relative entropy S(\rho_w^{\mathrm{vis}}\Vert \omega_w^{\mathrm{vis}}) then gives a local Clausius inequality:

\Delta S_{\mathrm{vN}}^{\mathrm{vis}} \ge \beta Q_{\mathrm{in}}^{\mathrm{vis}}<br /> \quad\Longleftrightarrow\quad<br /> \Delta S_{\mathrm{vN}}^{\mathrm{vis}} - \frac{1}{T} Q_{\mathrm{in}}^{\mathrm{vis}} \ge 0.

This is the QTT-native version of the thermodynamic Second Law in the visible sector. The Reality Dimension enters via the modular structure and the dial/KMS geometry; the entropy change and heat flow are controlled by how the visible world–cell state deviates from its anchored modular reference.

6. The five central boxed entropy-emergence laws

The entropic structure of QTT can be summarised by five boxed equations. Together, they encode how the Reality Dimension enforces finite entropy, finite entanglement, and a well-behaved Page curve:

  1. Area Law from Capacity (fundamental entropy bound)
\boxed{<br /> S_{\mathrm{QTT}} \;\le\; \frac{k_B A}{4 \tilde\ell^2}<br /> }
  1. Dynamic Page Curve Bound (entropy of radiation)
\boxed{<br /> S_{\rm rad}(t) \;\le\; S_{\mathrm{QTT}}<br /> }
  1. Curvature / Energy Density Ceiling → finite entropy
\boxed{<br /> \rho \;\le\; \rho_\ast<br /> }
  1. Capacity–Hadamard Conservation → finite entanglement
\boxed{<br /> \nabla_\mu \langle T^{\mu\nu} \rangle_{\rm ren} = 0<br /> }
  1. Four–Volume Quantisation → finite microstate count
\boxed{<br /> \Delta V_4 = 4\pi \tilde\ell^4<br /> }

Together, these five boxed relations say:

  • The total entropy is bounded by an area law set by the Planck–scale Reality–Dimension cell size \tilde\ell.
  • The entropy of radiation is always bounded by the QTT entropy budget, guaranteeing a well-behaved Page curve.
  • Curvature and energy density cannot exceed \rho_\ast, preventing entropy from diverging in high–curvature regimes.
  • Capacity–Hadamard conservation enforces finite entanglement within the Reality–Dimension ledger.
  • Four–volume is quantised in chunks of 4\pi \tilde\ell^4, giving a finite microstate count per region.

These are the central boxed QTT entropy–emergence laws, directly tied to the discrete geometry of the Reality Dimension.

7. Unified picture: Entropy as a Reality–Dimension charge

Putting it all together, QTT turns entropy into a sharply defined, geometric object:

  • Each world–cell in the Reality Dimension (each address w) carries a modular budget Q_w^{\mathrm{bundle}} = 2\pi.
  • Visible and hidden sectors share this budget, with visible entropy given by anchored modular charge Q_w(\rho_w \Vert \omega_w).
  • The total entropy is proportional to the number of active addresses, which grows because the Reality Dimension creates new world–cells over time.
  • Local thermodynamic behavior (Clausius inequality, KMS) emerges from the modular/dial structure at each address.
  • Area laws, Page-curve bounds, and finite entanglement follow from finite capacity and four–volume quantisation in the Reality Dimension.

From this viewpoint, the familiar Second Law is not a probabilistic accident. It is a statement about how the Reality Dimension continuously expands the ledger of world–cells, each with a fixed entropy budget, and how visible/hid shares of modular charge evolve under capacity–conserving dynamics.

Entropy, in QTT, is no longer an afterthought tacked onto mechanics. It is a primary Reality–Dimension charge attached to addresses in the world–cell ledger — and the arrow of time is written directly into how those addresses are created and filled.

Published by Quantum Traction Theory

Ali Attar

Join the Conversation

  1. Unknown's avatar

1 Comment

  1. Pingback: Solving the Three‑Body with Law of Endurance – QTT – Quantum Traction Theory

Leave a comment