QTT Thermopower: Capacity, Reality Dimension, and the thermoelectric field

10.5281/zenodo.17527179

In ordinary solid–state physics, a temperature gradient across a conductor can drive an electric field even when no net current flows. In linear response, this is written as the familiar thermoelectric or Seebeck law

Equation

E = Q ∇ T,

where Q is the Seebeck coefficient (thermopower). In Quantum Traction Theory (QTT), this macroscopic law is not just a phenomenological fit. It emerges from:

• the equilibrium of a capacity chemical potential,
• the fact that charge and heat are different dials of the same capacity ledger,
• and Planck–scale capacity bounds on electric fields and temperature gradients in each world–cell.

To avoid confusion with the QTT Absolute Clock T, we denote thermodynamic temperature by Θ. The classical law becomes

Equation

E = Q ∇Θ,

with Q the thermoelectric coefficient.

1. Classical Seebeck effect from electrochemical equilibrium

Consider charge carriers of charge q and number density n(x) in a conductor. Let μ(Θ,n) be the chemical potential per carrier and φ(x) the electric potential. The electrochemical potential is

Equation

tildeμ(x) = μ(Θ(x),n(x)) + q φ(x).

In static equilibrium with no net particle current, tildeμ must be spatially constant:

Equation

∇ tildeμ = 0.

Assuming a uniform carrier density (no accumulation), , we have

Equation

∇μ = ((∂μ)/(∂Θ))_n∇Θ.

The equilibrium condition becomes

Equation

((∂μ)/(∂Θ))_n∇Θ + q ∇φ = 0.

Using gives

Equation

E = (1)/(q)((∂μ)/(∂Θ))_n∇Θ.

This is usually rewritten in the form

Equation

Q = (1)/(q) ((∂μ)/(∂Θ))_n, E = Q ∇Θ.

This boxed equation is the standard microscopic definition of the Seebeck coefficient: the thermopower is given by the temperature derivative of the chemical potential per carrier, divided by the carrier charge.

2. QTT reinterpretation: chemical potential as capacity potential

QTT treats the chemical potential as a capacity potential. Each carrier corresponds to a dial configuration on a Planck–scale world–cell and carries:

• a U(1) dial charge

Equation

q = N_q e_0, N_q ∈ Z,

with the fundamental charge quantum; a thermal capacity per carrier , such that

Equation

dE_th = c_th dΘ;

a capacity chemical potential , the tick–energy cost to add one more carrier to the world–cell ensemble.

QTT identifies

Equation

μ(Θ,n) equiv μ_rm cap(Θ,n).

Then the Seebeck coefficient becomes

Equation

Q_QTT = (1)/(N_q e_0) ((∂μ_rm cap)/(∂Θ))_n.

So in QTT the thermoelectric coefficient is explicitly:

• “change of capacity energy per carrier per unit Θ,”
• divided by the dial charge per carrier .

In simple models, per carrier, so . QTT interprets as the natural ratio of a thermal capacity quantum to a dial charge quantum.

3. World–cell capacity bounds on 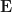E and

Equation

∇Θ

QTT also imposes finite capacity per world–cell, which bounds both the electric field and the temperature gradient.

The electromagnetic energy density in the lab is . The QTT space quantum volume is

Equation

V_SQ = 4π ℓ_P³,

and the universal tick energy is

Equation

E_ast = (ℏ)/(t̃) = (ℏ c)/(ℓ̃).

Requiring that a single space quantum never stores more than one tick energy gives

Equation

(1)/(2)ε_0 E² V_SQ ≤ E_ast Longrightarrow |E| ≤ E_max := sqrt((2E_ast)/(ε_0 V_SQ)).

Similarly, if a temperature gradient across one cell of size would change the thermal capacity by more than the available per–cell capacity, it is not allowed. This yields a material–dependent upper bound

Equation

|∇Θ| ≤ (∇Θ)_max.

Together with , these bounds imply

Equation

|Q_QTT| |∇Θ| ≤ E_max,

so for a given material (fixed ) the allowed temperature gradient is limited by world–cell capacity.

4. QTT thermoelectric law (all boxed relations)

Collecting everything, the QTT version of the thermoelectric law is:

Equation

E &= Q_QTT ∇Θ, [0.3em] Q_QTT &= (1)/(q) ((∂μ_rm cap)/(∂Θ))_n, q = N_q e_0, [0.3em] |E| &le E_max = sqrt((2E_ast)/(ε_0 V_SQ)), |∇Θ| le (E_max)/(|Q_QTT|).

This boxed law contains all of the QTT thermoelectric structure:

• The field–gradient relation
  Equation

  

  E = Q_QTT ∇Θ

  .

• The microscopic definition of as a capacity chemical–potential derivative per dial charge.
• Planck–regulated bounds on both |E| and arising from finite electromagnetic and thermal capacity per world–cell.

5. What thermopower means in QTT

From the QTT viewpoint, the Seebeck effect is no longer just “hot carriers diffuse, so an electric field appears.” Instead:

• Heat and charge are different dials of the same capacity carried by world–cell configurations.
• A temperature gradient tilts the thermal dial, changing the capacity chemical potential .
• The system restores equilibrium of electro–capacity by creating an electric potential gradient, i.e. an E field.
• All of this happens under strict Planck–scale capacity bounds on energy per cell and thermal gradients.

The classical law is still correct, but QTT exposes its deeper structure:

thermopower is the ratio of capacity energy per carrier to dial charge, and the resulting thermoelectric field is the Reality–Dimension–regulated response of a finite–capacity world–cell lattice.